ds xˆ h dx xˆ h dx xˆ h dx.
|
|
|
- Abner Bond
- 5 years ago
- Views:
Transcription
1 Lecture : Legedre Poyomias I (See Chapter i Boas) I the previous ectures we have focused o the (commo) case of d differetia equatios with costat coefficiets However, secod order differetia equatios with NON-costat coefficiets do arise i physics, especiay whe we cosider fuctios of 3 spatia dimesios, ie, whe we cosider fieds that satisfy partia differetia equatios Famiiar eampes are eectric ad magetic fieds, gravitatioa fieds ad the fieds that describe partices whe we quatize them We wat to discuss a eampe of that situatio ow This eampe is caed the Legedre equatio, which arises whe we cosider Lapace s equatio i 3-D with spherica coordiates (eg, reevat for ay probem described by a potetia, away from the sources, as i eectromagetism) Reca that i spherica coordiates we have r r si 0 r r r r si r si () Note, i particuar, the etra factors that appear both iside ad outside of the differetias due to the curviiear coordiates (see Chapter 0 i Boas, ad reca the discussio ast quarter ad the begiig of this quarter i Lecture 3, especiay i Appedi A) To uderstad how this factors arise cosider a ifiitesima ie eemet writte i terms of ifiitesima steps i each coordiate directio with appropriate coefficiets empoyig the otatio of Chapter 0 (these coefficiets carry the reevat iformatio to esure that each differetia eemet is a ie eemet), ds ˆ h d ˆ h d ˆ h d I rectaguar coordiates this form is particuary simpe, () h ds d ˆ ydy ˆ zdz ˆ : y h 3 z h3 (3) Thigs become more iterestig i curviiear coordiates For spherica coordiates we have Physics 8 Lecture Witer 009
2 r h ds rdr ˆ ˆ rd ˆ r si d : h r 3 h3 r si (4) I terms of these coefficiet factors the gradiet operator ooks ike U U U U ˆ ˆ ˆ 3 h h h3 3 (5) Note that the deomiator i each term is the correspodig eemet of distace from Eq () So i rectaguar coordiates we have the famiiar form U U U U ˆ yˆ zˆ, y z (6) whie i spherica coordiates we fid the more compicated epressio U ˆ U ˆ U U rˆ r r rsi (7) The correspodig divergece ad Lapacia operators are epressed as ad h h V h h V h h V V h h h 3 3 V r Vr si V, r r r si r si hh3 U hh 3 U hh U U h h h 3 h h 3 h 3 3 U U U r si r r r r si r si (8) (9) Physics 8 Lecture Witer 009
3 I each case we have dispayed the form with the epicit coefficiet factors, which coud be used to fid the same operators i other coordiates (eg, rectaguar or cyidrica), ad the specific spherica coordiate epressio As we have discussed earier the coefficiet factors i the umerator (ad deomiator) arise because, for curviiear coordiates, the divergece free basis vectors have the form (see eercise 09: i Boas) ˆ ˆ ˆ hh3 hh 3 hh 3 0 (0) Hece, before takig the divergece of a vector, we shoud be thikig of epressig it as V V ˆ ˆ V ˆ V 3 3 ˆ ˆ ˆ h h h h h h 3 h h V h h V h h V () Dottig the previousy defied gradiet operator (with aother factor of a h k i each term) resuts i the above epressio for the divergece, where these speciay defied basis vectors have zero divergece ˆ ˆ ˆ V h h V h h V h h V h h h h h h h h V h h V h h V h h h () A simiar argumet appies for the Lapacia operator For referece we shoud aso cosider the same epressios i cyidrica coordiates, Physics 8 Lecture 3 Witer 009
4 h ds ˆ d ˆ d zdz ˆ : h, 3 z h3 U U U U ˆ ˆ ˆ 3 h h h 3 3 U ˆ U U ˆ zˆ, z h h V h h V h h V V h h h Vz V V, z hh3 U hh 3 U hh U h h h 3 h h 3 h z U U U U 3 3 (3) I ay case, it shoud ow be cear that o-costat coefficiets aturay arise i physics i 3-D A powerfu too for addressig partia differetia equatios with o-costat coefficiets is (our od fried) the techique of separatio of variabes (Here we are separatig the depedece o the various idepedet variabes, rather tha separatig depedet from idepedet variabes as i Lecture 4) Goig back to spherica coordiates as i Eq (), we start with the separatio of r,, R r (this is ot the theta fuctio discussed variabes Asatz, earier), ad focus (for ow) o the case a costat (o aguar mometum i the z-directio ad hece o depedece) If we substitute this Asatz ito Eq () ad the divide the etire equatio by r,, we fid that Lapace s equatio spits ito two distict terms, oe depedig o r aoe ad oe depedig o aoe (we wi come back to the case of depedece) Note i particuar that such a separated equatio ca be satisfied if ad oy if the sides of the equatio are each equa to the same costat (ie, idepedet of a of the idepedet variabes) We choose to epress this resut as Physics 8 Lecture 4 Witer 009
5 d r d Rr d si d, R r dr dr si d d (4) where we have abeed the costat by for ater coveiece With the (stadard) chage of variabe cos, d d si,, we obtai Legedre s equatio for the poar age ( ) depedece i Lapace s equatio, d d d 0 d d d 0 d d d d 0 d d (5) This ast form is the caoica form (ie, the coefficiet of the highest derivative is uity) The ew ad iterestig feature is the (ie, cos ) depedece of the other coefficiets To uderstad the overa behavior of the soutios to such equatios, we first cosider the questio of where these coefficiet fuctios are siguar (thought of as a aaytic fuctio of a potetiay compe argumet as i Lecture 7) This behavior wi determie the possibe siguarity structure of the soutios I particuar, we see that, based o the siguarity structure of the coefficiet fuctios i Eq (5), 0 is a reguar poit (o siguarities i the coefficiet fuctios), whie are reguar siguar poits (oy simpe poes i the coefficiet fuctios) (Note the ew termioogy!) Sice the coefficiets are we behaved at 0, we epect to be abe to fid soutios of this equatio i terms of Tayor series epasios about 0 However, the siguarities i the coefficiet fuctios te us that we wi have to worry about whether these series epasios coverge or ot at From the stadpoit of the physics, there is othig specia about these poits (just the orth ad south poes,, 0, ) The physicay iterestig soutios wi (typicay) be the oes that are aaytic (we behaved) at = 0 ad, ie, we wat the series epasio that coverges o the fu cosed iterva (ie, our boudary coditios are that we wat fuctios that are we behaved at ) Physics 8 Lecture 5 Witer 009
6 ASIDE: Note that, sice the origia equatio is secod order, we epect aso a secod soutio, which wi have distictive, o-aaytic behavior at We wi retur to this poit at the ed of the ecture As we wi shorty see, this combiatio of a differetia equatio (Legedre) ad boudary coditios (aaytic o the cosed iterva) is typica of our efforts to describe physica systems ad eads to a eigevaue probem As i our earier studies of eigevaue probems i terms of matrices, soutios wi eist oy for specific (discrete) vaues of the parameter (the eigevaue) ad, moduo the (famiiar) questio of ormaizatio, there wi be a uique eigefuctio for each vaue of The correspodig eigefuctios (the Legedre poyomias) wi costitute a compete ad orthogoa set of fuctios of o the iterva (agai simiar to our earier eigevaue probem studies) Thus our efforts to fid basis fuctios of various kids are ow ceary coected to our uderstadig of eigevaue probems We wi aso use this eampe of Legedre poyomias to see how our kowedge of the differetia equatio ca be tured ito kowedge about the properties of the resutig eigefuctios To proceed we defie a power series Asatz (the method of udetermied coefficiets) c, (6) 0 ad substitute ito Legedre s equatio, Eq (5) As usua we isoate each idividua power of to fid (ie, sice the right-had-side vaishes, each idividua coefficiet i the power series must vaish) c c c c c c c c c c 0 Physics 8 Lecture 6 Witer 009
7 c c c c 0 a c c (7) Note how we have redefied the subscripts o the coefficiets of some of the terms i the third ie ( i the first term of the first ie, where iitiay the = 0 ad = terms vaish, so that c c ad ) i order to isoate a sige power of i the third ie (previous page) To satisfy the equatio i the secod ie power-by-power, the coefficiet of the power must vaish for a ad thus the origia coefficiets c must i tur satisfy the recursio reatio i the ast ie (kowig c aows us to cacuate c ) The fact that jumps by i the recursio reatio tes us, as epected o both geera ad symmetry grouds, that we have two idepedet kids of soutios Oe ivoves oy eve powers of ad is thus eve i The other ivoves oy odd powers ad is odd i We have m m m, m (8) c c eve odd m0 m0 Oce we kow c 0 a terms i the eve series are kow from the recursio reatio, whie the odd series is fuy specified by c ad the recursio reatio Net cosider the behavior of the series as The famiiar ratio test says that, usig the recursio reatio, m cm m m m m m m m m c m m m m m m m m m (9) Thus i the imit we vioate the usua test for covergece (due to the absece of the m m term) ad the series wi diverge uess the ifiite series is trucated, ie, uess it is actuay a fiite series Thus, if we demad a soutio that is we behaved at the edpoits of the iterva, we must demad that the series trucates This resut is, i tur, easiy arraged as a eigevaue costrait If, istead of beig arbitrary, we require that is a iteger 0, the if foows from the recursio c, or c 0, Thus for the reatio for the coefficiets that Physics 8 Lecture 7 Witer 009
8 eigevaue, with a iteger vaue ( 0), the correspodig eigefuctio is a poyomia of degree (highest power) These are the much oved Legedre poyomias We kow from the form of the recursio reatio for the coefficiets that for odd (eve), the correspodig poyomia ivoves oy odd (eve) powers of ad is thus a odd (eve) fuctio of The ormaizatio of the poyomias is fied (historicay ad arbitrariy) by the costrait P (0) Note that it foows immediatey from the odd/eve properties of the poyomias that P We ca use the ormaizatio costrait ad the recursio reatio for the coefficiets to easiy fid the first few poyomias: 0 : P c, 0 0 : P c, P c P, c 6 P c P c c : 0 3, c0 P 3, c P c P c c : 3, 3 c 3 P3 5 3, c 0 c :, P4 c0 0, c c P4 c0 6 4 P () The behaviors of these poyomias as fuctios of are iustrated i the foowig figures Physics 8 Lecture 8 Witer 009
9 P0 P P P P4 - The other Legedre poyomias ca be (aboriousy) costructed by foowig this ie of cacuatio, but we wat to deveop more powerfu meas to study these fuctios, usig the toos we have eared i this course Here we wi use what we have recety eared to obtai a variety of represetatios for ad isights ito the properties of the Legedre poyomias (see especiay the eampes i Appedi B) By simpe iteratio of the recursio reatio for the coefficiets we fid the foowig cosed epressio for the poyomias, Physics 8 Lecture 9 Witer 009
10 P, 0!!! ()! where the symbo stads for the argest iteger i (ie, = m both for = m ad for = m+) We recogize the form of the terms as arisig from takig derivatives,! d! d, (3) which resuts i a biomia series that we ca sum (ote the simpificatio of the upper imit o the sum after we factor out the derivatives) Thus after some reorgaizatio we fid P d d 0!! d!! d 0!! (4) d! d a biomia series This formua, Rodrigues formua, is easy to use i terms of Leibiz s rue, which says to thik of appyig mutipe derivatives to a product i terms of a biomia of two derivatives, oe actig o each factor of the product, ad the epad the biomia Physics 8 Lecture 0 Witer 009
11 d d d d d U d V U V U V d d d U V U V d d d (5) d d d U V U V d d d With the idetificatio U, V we ca easiy check the vaues of the poyomias at the ed poits For the case, the resut wi come oy from terms with o factors of, which eads uiquey to the ast term i the epasio above where a of the derivatives act o V, d P!! d! (6) At the opposite edpoit the oy ozero cotributio is the first term i the epasio where a of the derivatives act o U, d P!! d! (7) We ca proceed to ear more about the Legedre poyomias by ivokig our kowedge of aaytic fuctios Cauchy, combied with Rodrigues, aows us first to epress the Legedre poyomia as a cotour itegra about the poit i the compe z pae, ie, is iside C, ad the to take the derivatives iside the itegra to fid d d z P dz! d! d i z z dz i z C, C (8) Physics 8 Lecture Witer 009
12 which is ofte caed Schäfi s itegra formua Our et step is to make a specific choice for the cotour C, a choice attributed to Lapace Let C be a circe of radius about the poit (admittedy umotivated iitiay, but remember o soap operas back the!) O such a circe we have i z e,0 i dz e id z id z e e i i i i i i e z e e e cos cos (9) Substitutig these epressios ito Eq (8) we obtai Lapace s itegra formua for the Legedre poyomias, z cos P z id i z C P d cos d cos 0 0 (30) This ast resut becomes particuary usefu whe we cosider defiig a geeratig fuctio for the Legedre poyomias At the cost of itroducig this ew cocept, the geeratig fuctio, we wi obtai some very smart but azy resuts I geera, a geeratig fuctio is a fuctio of two variabes such that the coefficiets of the Tayor series epasio i oe of the variabes are iterestig fuctios of the other variabe I our case we wat h, h P P h, (3) 0! h h0 Physics 8 Lecture Witer 009
13 With this goa i mid we ca use the previous itegra epressio to obtai a sum we ca perform, ie, a geometric series h, h d cos 0 0 d h 0 0 d cos 0 h cos (3) To perform the itegra we go back to compe cotour itegratio otatio with the defiitios (the cotour is the uit circe), dz i,cos z z z e d iz dz h, i z z h z z z dz i z h z h h (33) The quadratic epressio i the deomiator wi vaish at two poits i the compe z pae, ie, there are two poes, z h h h h h h h h h h h h h h h, z z z z (34) Note that, sice the product of the magitudes of the two compe umbers is uity, we are guarateed that oe of the poes is iside of our uit circe cotour ad the other oe is outside Thus we ca evauate the itegra i terms of the residue at the Physics 8 Lecture 3 Witer 009
14 iside poe (you shoud covice yoursef that the cocusio that oy oe poe cotributes is idepedet of the precise vaues of the variabes h ad, whie here we thik about sma h ad z as the poe iside), h, dz iresz z i h z z z z z i i h z z h h h h h h (35) To test our uderstadig of this epressio cosider usig it to evauate the Legedre poyomias at the edpoits ad the origi, h,, h P h P h h h 0 0 h, h h h h 0 0 P h P, m h,0 h 0 0 P h h m 0 m! 0 : odd P 0 : eve m m (36) To appreciate this ast epressio we eed to reca the properties of the Gamma fuctio (see Sectio 3 i Boas), Physics 8 Lecture 4 Witer 009
15 !, iteger (37) We ca aso use the geeratig fuctio to derive recursio reatios betwee the poyomias For eampe, if foows from the form of the geeratig fuctio i Eq (35) that h, h h 3 h h h h h h, (38) Usig the series defiitio of the geeratig fuctio, Eq (35), ad this epressio, Eq (38), we ca obtai two epressios for the same fuctio, h, h ad h h h h h P 0 h h h P h h h P 0 0 h P h P P h, h h h h h h P h, h P h P 0 0 (39) Equatig the coefficiets of the same power of h i each of the fia epressios, we fid (see Eq 58a i Boas) that (this is for, for 0 we have the trivia resut P P0) P P P P P P P P 0 (40) Physics 8 Lecture 5 Witer 009
16 Aother usefu reatio (see Eq 58d i Boas ad the et Lecture) arises from performig the foowig (currety umotivated) operatios o the geeratig fuctio i Eq (35) We have h 3 h h h h h h h h h, h h h h h h h h P h P, h 0 0 (4) ad h h h 3 3 h h h h h h h h h h h h h P h h 0, h P h P h P h P (4) Thus Eqs (4) ad (4) are represetatios of the same quatity ad we ca agai equate the coefficiets of h i the equatios This yieds the usefu idetity P P P P, 0,, 0 (43) which we ca quicky cofirm agrees with the epicit epressios for sma i Eq (): P dp d d d, 0 0 3P 3 dp d dp d d 3 d, etc This resut is very usefu for performig itegras of the P sice we ca chage Physics 8 Lecture 6 Witer 009
17 P ito derivatives of other poyomias, ad itegras of derivatives are simpe (for the smart but azy) As a eampe of how we ca use the geeratig fuctio for the Legedre poyomias i physics we appy it to the famiiar r potetia, which appears i E&M ad gravity ASIDE: This famiiar r form arises because it is the behavior of the Gree s fuctio for the ihomogeeous Lapace equatio (Poisso s Equatio) G r, r r r G r, r 4 r r (44) We ca verify that this epressio has the correct behavior by usig our kowedge of vector aaysis, r sphere rˆ ˆ 4 r 4 r 4 r 4 r 0 r 0, 4r 4r r rˆ d d 4r 4r sphere rˆ 4 r d 4 r 4 r sphere rˆ (45) These properties are precisey those of the 3-D Dirac deta fuctio Now cosider a observer at poit r ad a poit charge (or mass) at the poit R i some coordiate system, Q Q Q V r, R Gr, R, (46) 4 R r 4 R r rrcos Physics 8 Lecture 7 Witer 009
18 where is the age betwee r ad R For r R (the far regio ) we epad i powers of h R r (sice it is ess tha ) usig Eq (35) V r, R Q 4 r R r R r cos 0 0 Q R P 4 r 0 r cos (47) I the opposite imit, r R, we simpy epad i terms of powers of h r R Fiay cosider the potetia outside of a cotiuous charge distributio, R, of 3 fiite etet Agai we have r R Q d R R ) ad write ( R R 3 3 Vout r d R d R 4 0 R r 4 0 R r rrcos 4 r 0 r 0 3 d R R P R cos We recogize this epressio as the usua muti-poe momet epasio i a coordiate system with the z-directio aog r The case 0 is the tota charge, whie is the dipoe momet, etc Physics 8 Lecture 8 Witer 009 (48) We cose this discussio by otig that, as epected, there is a secod soutio to Legedre s equatio, which, uike the poyomias above, is poory behaved for sma vaues of, but is we behaved for arge (where is apparety o oger iterpreted as the cosie of a rea age) Thus the secod soutio does ot satisfy the boudary coditios we imposed above (i fact, the secod soutio has ogarithmic brach poits at ) Reca that for arge vaues (ote that, sice the P are just poyomias, there is o particuar probem with takig ), we epect P The secod soutio, sometimes writte as (see eercise :4 i Appedi B) dz Q P, (49) z P z
19 behaves asymptoticay ike Q (or stricty its rea part does) This differece betwee the asymptotic behaviors of the two soutios to a secod order homogeeous equatio is geeric Oe soutio is typicay we behaved for sma vaues of the argumet but ot arge vaues, whie the secod soutio ehibits the opposite behavior Eampes of these secod soutios (see Appedi B) are, with the aaytic structure chose by Boas, Q Q 0, (50) Note that these fuctios ehibit (ogarithmic) brach poits (siguarities) at where the usua Legedre Poyomias are reguar (by costructio) Due to these brach poits we shoud be carefu to defie the Q i the compe pae, ie, where do we put the brach cut? A covetioa choice is to put the brach cut aog the rea ais betwee z ad z With this choice the fuctio Q z is rea aog the rea ais z, but compe for z This choice correspods to the forms Q Q 0 z z z, z z z, z (5) which have the advertised asymptotic behavior Q aog the rea ais The epressios ehibited i Boas ad i Eq (50) evauated aog the rea ais for ca be thought of as the average of Eq (5) o the two sides of the brach cut or simpy the rea part Aterativey we ca thik of Eq (50) as defiig aaytic fuctios that have the brach cuts from z to z (aog the positive rea ais) ad from z to z (aog the egative rea ais) I this case the asymptotic behavior picks up a imagiary part, the sig of which depeds o whether we are above or beow the cut ad i which directio we take the asymptotic imit Physics 8 Lecture 9 Witer 009
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
19 Fourier Series and Practical Harmonic Analysis
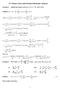 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Chem 442 Review for Exam 1. Hamiltonian operator in 1 dimension: ˆ d first term is kinetic energy, second term is potential energy
 Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
x a x a Lecture 2 Series (See Chapter 1 in Boas)
 Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Apply change-of-basis formula to rewrite x as a linear combination of eigenvectors v j.
 Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
On the Diophantine equation x 2 2 ˆ y n
 Arch. Math. 74 (000) 50±55 000-889/00/05050-06 $.70/0 Birkhäuser Verag, Base, 000 Archiv der Mathematik O the Diohatie equatio x ˆ y By B. SURY Abstract. We give a eemetary roof of the fact that the oy
Arch. Math. 74 (000) 50±55 000-889/00/05050-06 $.70/0 Birkhäuser Verag, Base, 000 Archiv der Mathematik O the Diohatie equatio x ˆ y By B. SURY Abstract. We give a eemetary roof of the fact that the oy
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
U8L1: Sec Equations of Lines in R 2
 MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
Discrete Fourier Transform
 Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
mx bx kx F t. dt IR I LI V t, Q LQ RQ V t,
 Lecture 5 omplex Variables II (Applicatios i Physics) (See hapter i Boas) To see why complex variables are so useful cosider first the (liear) mechaics of a sigle particle described by Newto s equatio
Lecture 5 omplex Variables II (Applicatios i Physics) (See hapter i Boas) To see why complex variables are so useful cosider first the (liear) mechaics of a sigle particle described by Newto s equatio
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
9.3 Power Series: Taylor & Maclaurin Series
 9.3 Power Series: Taylor & Maclauri Series If is a variable, the a ifiite series of the form 0 is called a power series (cetered at 0 ). a a a a a 0 1 0 is a power series cetered at a c a a c a c a c 0
9.3 Power Series: Taylor & Maclauri Series If is a variable, the a ifiite series of the form 0 is called a power series (cetered at 0 ). a a a a a 0 1 0 is a power series cetered at a c a a c a c a c 0
GENERATING FUNCTIONS
 GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Orthogonal transformations
 Orthogoal trasformatios October 12, 2014 1 Defiig property The squared legth of a vector is give by takig the dot product of a vector with itself, v 2 v v g ij v i v j A orthogoal trasformatio is a liear
Orthogoal trasformatios October 12, 2014 1 Defiig property The squared legth of a vector is give by takig the dot product of a vector with itself, v 2 v v g ij v i v j A orthogoal trasformatio is a liear
Z ß cos x + si x R du We start with the substitutio u = si(x), so du = cos(x). The itegral becomes but +u we should chage the limits to go with the ew
 Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
ECE Notes 6 Power Series Representations. Fall 2017 David R. Jackson. Notes are from D. R. Wilton, Dept. of ECE
 ECE 638 Fall 7 David R. Jackso Notes 6 Power Series Represetatios Notes are from D. R. Wilto, Dept. of ECE Geometric Series the sum N + S + + + + N Notig that N N + we have that S S S S N S + + +, N +
ECE 638 Fall 7 David R. Jackso Notes 6 Power Series Represetatios Notes are from D. R. Wilto, Dept. of ECE Geometric Series the sum N + S + + + + N Notig that N N + we have that S S S S N S + + +, N +
2 Geometric interpretation of complex numbers
 2 Geometric iterpretatio of complex umbers 2.1 Defiitio I will start fially with a precise defiitio, assumig that such mathematical object as vector space R 2 is well familiar to the studets. Recall that
2 Geometric iterpretatio of complex umbers 2.1 Defiitio I will start fially with a precise defiitio, assumig that such mathematical object as vector space R 2 is well familiar to the studets. Recall that
Rational Points over Finite Fields on a Family of Higher Genus Curves and Hypergeometric Functions. Yih Sung
 TAIWANESE JOURNAL OF MATHEMATICS Vo. xx, No. x, pp. 1 25, xx 20xx DOI: 10.11650/tjm.xx.20xx.7724 This paper is avaiabe oie at http://joura.tms.org.tw Ratioa Poits over Fiite Fieds o a Famiy of Higher Geus
TAIWANESE JOURNAL OF MATHEMATICS Vo. xx, No. x, pp. 1 25, xx 20xx DOI: 10.11650/tjm.xx.20xx.7724 This paper is avaiabe oie at http://joura.tms.org.tw Ratioa Poits over Fiite Fieds o a Famiy of Higher Geus
Chapter 7: Numerical Series
 Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Physics 116A Solutions to Homework Set #1 Winter Boas, problem Use equation 1.8 to find a fraction describing
 Physics 6A Solutios to Homework Set # Witer 0. Boas, problem. 8 Use equatio.8 to fid a fractio describig 0.694444444... Start with the formula S = a, ad otice that we ca remove ay umber of r fiite decimals
Physics 6A Solutios to Homework Set # Witer 0. Boas, problem. 8 Use equatio.8 to fid a fractio describig 0.694444444... Start with the formula S = a, ad otice that we ca remove ay umber of r fiite decimals
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Chapter 6 Overview: Sequences and Numerical Series. For the purposes of AP, this topic is broken into four basic subtopics:
 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
Mathematical Series (You Should Know)
 Mathematical Series You Should Kow Mathematical series represetatios are very useful tools for describig images or for solvig/approimatig the solutios to imagig problems. The may be used to epad a fuctio
Mathematical Series You Should Kow Mathematical series represetatios are very useful tools for describig images or for solvig/approimatig the solutios to imagig problems. The may be used to epad a fuctio
Machine Learning for Data Science (CS 4786)
 Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Chapter 6: Numerical Series
 Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Stat 543 Exam 3 Spring 2016
 Stat 543 Exam 3 Sprig 06 I have either give or received uauthorized assistace o this exam. Name Siged Date Name Prited This exam cosists of parts. Do at east 8 of them. I wi score aswers at 0 poits apiece
Stat 543 Exam 3 Sprig 06 I have either give or received uauthorized assistace o this exam. Name Siged Date Name Prited This exam cosists of parts. Do at east 8 of them. I wi score aswers at 0 poits apiece
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
Linear Differential Equations of Higher Order Basic Theory: Initial-Value Problems d y d y dy
 Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
CALCULUS BASIC SUMMER REVIEW
 CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
1. Hydrogen Atom: 3p State
 7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Lecture 6: Integration and the Mean Value Theorem
 Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech - Fall, 2011 1 Radom Questios Questio 1.1. Show that ay positive ratioal umber ca be writte as the sum of
Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech - Fall, 2011 1 Radom Questios Questio 1.1. Show that ay positive ratioal umber ca be writte as the sum of
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Lecture 6: Integration and the Mean Value Theorem. slope =
 Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
(a) (b) All real numbers. (c) All real numbers. (d) None. to show the. (a) 3. (b) [ 7, 1) (c) ( 7, 1) (d) At x = 7. (a) (b)
 Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
8. Applications To Linear Differential Equations
 8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
THE SOLUTION OF NONLINEAR EQUATIONS f( x ) = 0.
 THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
subcaptionfont+=small,labelformat=parens,labelsep=space,skip=6pt,list=0,hypcap=0 subcaption ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, 2/16/2016
 subcaptiofot+=small,labelformat=pares,labelsep=space,skip=6pt,list=0,hypcap=0 subcaptio ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, /6/06. Self-cojugate Partitios Recall that, give a partitio λ, we may
subcaptiofot+=small,labelformat=pares,labelsep=space,skip=6pt,list=0,hypcap=0 subcaptio ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, /6/06. Self-cojugate Partitios Recall that, give a partitio λ, we may
SECTION 2 Electrostatics
 SECTION Electrostatics This sectio, based o Chapter of Griffiths, covers effects of electric fields ad forces i static (timeidepedet) situatios. The topics are: Electric field Gauss s Law Electric potetial
SECTION Electrostatics This sectio, based o Chapter of Griffiths, covers effects of electric fields ad forces i static (timeidepedet) situatios. The topics are: Electric field Gauss s Law Electric potetial
A Note on Some Approximation Kernels on the Sphere
 A Note o Some Approximatio Keres o the Sphere Peter Graber Dedicated to Ia H. Soa o the occasio of his 80 th birthday. Abstract We produce precise estimates for the Kogbetiatz kere for the approximatio
A Note o Some Approximatio Keres o the Sphere Peter Graber Dedicated to Ia H. Soa o the occasio of his 80 th birthday. Abstract We produce precise estimates for the Kogbetiatz kere for the approximatio
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
INTEGRATION BY PARTS (TABLE METHOD)
 INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
f t dt. Write the third-degree Taylor polynomial for G
 AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
Subject: Differential Equations & Mathematical Modeling-III
 Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
MSM203a: Polynomials and rings Chapter 3: Integral domains and fields
 MSM203a: Poyomias ad rigs Chapter 3: Itegra domais ad fieds Richard Kaye Autum 2013 Note: These prited hadouts are iteded to suppemet the materia provided i ectures. They are ot sufficiet o their ow. This
MSM203a: Poyomias ad rigs Chapter 3: Itegra domais ad fieds Richard Kaye Autum 2013 Note: These prited hadouts are iteded to suppemet the materia provided i ectures. They are ot sufficiet o their ow. This
Recitation 4: Lagrange Multipliers and Integration
 Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Question 1: The magnetic case
 September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
Subject: Differential Equations & Mathematical Modeling -III. Lesson: Power series solutions of Differential Equations. about ordinary points
 Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Fundamental Concepts: Surfaces and Curves
 UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
Linear Regression Demystified
 Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
U8L1: Sec Equations of Lines in R 2
 MCVU Thursda Ma, Review of Equatios of a Straight Lie (-D) U8L Sec. 8.9. Equatios of Lies i R Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio
MCVU Thursda Ma, Review of Equatios of a Straight Lie (-D) U8L Sec. 8.9. Equatios of Lies i R Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio
Notes on iteration and Newton s method. Iteration
 Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
The multiplicative structure of finite field and a construction of LRC
 IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
10.6 ALTERNATING SERIES
 0.6 Alteratig Series Cotemporary Calculus 0.6 ALTERNATING SERIES I the last two sectios we cosidered tests for the covergece of series whose terms were all positive. I this sectio we examie series whose
0.6 Alteratig Series Cotemporary Calculus 0.6 ALTERNATING SERIES I the last two sectios we cosidered tests for the covergece of series whose terms were all positive. I this sectio we examie series whose
TECHNIQUES OF INTEGRATION
 7 TECHNIQUES OF INTEGRATION Simpso s Rule estimates itegrals b approimatig graphs with parabolas. Because of the Fudametal Theorem of Calculus, we ca itegrate a fuctio if we kow a atiderivative, that is,
7 TECHNIQUES OF INTEGRATION Simpso s Rule estimates itegrals b approimatig graphs with parabolas. Because of the Fudametal Theorem of Calculus, we ca itegrate a fuctio if we kow a atiderivative, that is,
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Physics 324, Fall Dirac Notation. These notes were produced by David Kaplan for Phys. 324 in Autumn 2001.
 Physics 324, Fall 2002 Dirac Notatio These otes were produced by David Kapla for Phys. 324 i Autum 2001. 1 Vectors 1.1 Ier product Recall from liear algebra: we ca represet a vector V as a colum vector;
Physics 324, Fall 2002 Dirac Notatio These otes were produced by David Kapla for Phys. 324 i Autum 2001. 1 Vectors 1.1 Ier product Recall from liear algebra: we ca represet a vector V as a colum vector;
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 525: Lecture 5. January 18, 2018
 Math 525: Lecture 5 Jauary 18, 2018 1 Series (review) Defiitio 1.1. A sequece (a ) R coverges to a poit L R (writte a L or lim a = L) if for each ǫ > 0, we ca fid N such that a L < ǫ for all N. If the
Math 525: Lecture 5 Jauary 18, 2018 1 Series (review) Defiitio 1.1. A sequece (a ) R coverges to a poit L R (writte a L or lim a = L) if for each ǫ > 0, we ca fid N such that a L < ǫ for all N. If the
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Random Models. Tusheng Zhang. February 14, 2013
 Radom Models Tusheg Zhag February 14, 013 1 Radom Walks Let me describe the model. Radom walks are used to describe the motio of a movig particle (object). Suppose that a particle (object) moves alog the
Radom Models Tusheg Zhag February 14, 013 1 Radom Walks Let me describe the model. Radom walks are used to describe the motio of a movig particle (object). Suppose that a particle (object) moves alog the
Problem Cosider the curve give parametrically as x = si t ad y = + cos t for» t» ß: (a) Describe the path this traverses: Where does it start (whe t =
 Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
Polynomial Functions and Their Graphs
 Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
Taylor Polynomials and Taylor Series
 Taylor Polyomials ad Taylor Series Cotets Taylor Polyomials... Eample.... Eample.... 4 Eample.3... 5 Eercises... 6 Eercise Solutios... 8 Taylor s Iequality... Eample.... Eample.... Eercises... 3 Eercise
Taylor Polyomials ad Taylor Series Cotets Taylor Polyomials... Eample.... Eample.... 4 Eample.3... 5 Eercises... 6 Eercise Solutios... 8 Taylor s Iequality... Eample.... Eample.... Eercises... 3 Eercise
R is a scalar defined as follows:
 Math 8. Notes o Dot Product, Cross Product, Plaes, Area, ad Volumes This lecture focuses primarily o the dot product ad its may applicatios, especially i the measuremet of agles ad scalar projectio ad
Math 8. Notes o Dot Product, Cross Product, Plaes, Area, ad Volumes This lecture focuses primarily o the dot product ad its may applicatios, especially i the measuremet of agles ad scalar projectio ad
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
ECE-S352 Introduction to Digital Signal Processing Lecture 3A Direct Solution of Difference Equations
 ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
Machine Learning for Data Science (CS 4786)
 Machie Learig for Data Sciece CS 4786) Lecture 9: Pricipal Compoet Aalysis The text i black outlies mai ideas to retai from the lecture. The text i blue give a deeper uderstadig of how we derive or get
Machie Learig for Data Sciece CS 4786) Lecture 9: Pricipal Compoet Aalysis The text i black outlies mai ideas to retai from the lecture. The text i blue give a deeper uderstadig of how we derive or get
5th International Conference on Advanced Design and Manufacturing Engineering (ICADME 2015)
 5th Iteratioa Coferece o Advaced Desig ad Maufacturig Egieerig (ICADME 15) Series form soutio for a graded composite strip with eastic variatio i spa directio Qig Yag 1,,a *, Weipig Liu 1,b, Muhuo Yu,c,
5th Iteratioa Coferece o Advaced Desig ad Maufacturig Egieerig (ICADME 15) Series form soutio for a graded composite strip with eastic variatio i spa directio Qig Yag 1,,a *, Weipig Liu 1,b, Muhuo Yu,c,
Solutions to Homework 1
 Solutios to Homework MATH 36. Describe geometrically the sets of poits z i the complex plae defied by the followig relatios /z = z () Re(az + b) >, where a, b (2) Im(z) = c, with c (3) () = = z z = z 2.
Solutios to Homework MATH 36. Describe geometrically the sets of poits z i the complex plae defied by the followig relatios /z = z () Re(az + b) >, where a, b (2) Im(z) = c, with c (3) () = = z z = z 2.
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
APPENDIX F Complex Numbers
 APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
